In my previous post, I talked some basic stuff about naive bidirectional path tracing. However it is hard to show any real value since there are always too much noise comparing with best solutions depending on the scene to be rendered. That is because the contribution of each specific path is not properly weighted. And multiple importance sampling can be the key to the issue, the following comparison shows big difference between different methods. All of the images are generated with my open-source renderer.

Those images are generated with rough the same amount of time. No doubt about it, MIS BDPT dominates among all those results. It is less noisy and shows good caustics. Although light tracing can also shows good caustics, it is far from a practical algorithm due to the noise in the rest of the scene, not to mention it almost failed to show any radiance value on the glass monkey head. Traditional path tracing algorithm shows no caustics at all, not because it is a biased algorithm. It is unbiased for sure, however it just converges to the correct caustics in a unreasonable speed. Naive bidirectional path tracing also has roughly same amount of noise, however it also has dimmer monkey head because light tracing doesn’t do a good job on it. In other words, bidirectional path tracing barely reveals any value without MIS.

I searched a lot of materials about MIS in BDPT, however there are only quite limited materials on the internet. Although some open source renderers, like luxrender, give detailed implementation, most of them doesn’t give any insight in the math behind it, without which one can be quickly confused by its code. SmallVCM expends the algorithm further, offering a better solution over MIS BDPT and it has detailed paper on the math. However it is a little complex for someone who just wants to figure out how to do MIS BDPT. Eric Veach’s thesis gives the best explanation on MIS in BPDT,  sadly it doesn’t go further with MIS implementation. In this blog, I’m gonna talk something about MIS in bidirectional path tracing. Most of the theory comes from this paper.

PDF of a Specific Path

To use MIS in BDPT, it is very important to evaluate pdf of a specific path accurately. In my previous post, I mentioned the path pdf in path tracing. In a bidirectional path tracing algorithm, it is more complex since the path starts from both sides. However the theory stays similar, we just need to be careful with marginal conditions.

I’m gonna use the term in the SmallVCM paper because it is more elegant and easy to read. For a path starting from one side, we define the forward pdf term:

$$ \tag{1} \overrightarrow{p_i}(\bar{y}) = \begin{cases} p_a(\bar{y})&:i=0 \\ \overrightarrow{p_{\sigma , i}}(\bar{y})\overrightarrow{g_i}(\bar{y})&:otherwise \end{cases} $$ $$ \tag{2} \overrightarrow{p_{\sigma , i}}(\bar{y}) =\begin{cases} {p_{\sigma}}(p_0\rightarrow p_1)&:i=1 \\ {p_{\sigma}}(p_{i-2}\rightarrow p_{i-1} \rightarrow p_{i})&:i\ge 2 \end{cases}$$ $$ \tag{3} \overrightarrow{g_i}(\bar{y}) = \dfrac{cos \theta_{i\rightarrow i-1}}{\|y_i - y_{i-1} \|^2}$$

$ p_{\sigma} $ denotes the pdf w.r.t solid angle, $ p_a $ represents the pdf w.r.t area. For the first $ p_{\sigma} $ , it is defined the type of light sources or camera sensor and brdf defines the rest of them. The $ \overrightarrow{g} $ term converts the pdf measured from solid angle to area. With these terms defined, we have the pdf of a specific path starting from one side with s vertices, including the vertex on light sources or camera sensor, as the following one:

$$ \tag{4} p_s(\bar{y}) = \prod_{i=0}^{s-1}\overrightarrow{p_i}(\bar{y})$$

The reverse pdf of sub-path starting from the other side is quite similar with the above ones. For simplicity, they are listed here:

$$ \tag{5} \overleftarrow{p_i}(\bar{y}) = \begin{cases} p_a(\bar{y})&:i=k \\ \overleftarrow{p_{\sigma , i}}(\bar{y})\overleftarrow{g_i}(\bar{y})&:otherwise \end{cases}$$ $$ \tag{6} \overleftarrow{p_{\sigma , i}}(\bar{y}) = \begin{cases} {lr}{p_{\sigma}}(p_{k-1}\leftarrow p_k)&:i={k-1} \\ {p_{\sigma}}(p_{i}\leftarrow p_{i+1} \leftarrow p_{i+2})&:i\le{k - 2} \end{cases} $$ $$ \tag{7} \overleftarrow{g_i}(\bar{y}) = \dfrac{cos \theta_{i\rightarrow i+1}}{\|y_i - y_{i+1} \|^2} $$ $$ \tag{8} p_t(\bar{y}) = \prod_{i=k+1-t}^{k}\overleftarrow{p_i}(\bar{y}) $$

k is one less than the total number of vertices (including eye and light vertices) in the path, counting the two sub-path of light path and eye path. The different direction denotes that path is traced from a different direction other than the above one. Now we have the pdf of connecting two separate paths generated from each direction:

$$ \tag{9} p_{s,t}=p_s(\bar{y})p_t(\bar{y}) $$

Calculating this value in an accurate manner is not only particularly important for evaluating the Monte Carlo integral, but also a must have for multiple importance sampling factor evaluation.

MIS weight

For a naive bidirectional path tracer, the weight for connecting two sub-paths is simply 1/(s+t+1) where s is the number of vertices in the eye sub-path and t is the number of vertices in the light sub-path, both counting the first vertex sampled on light source or camera sensor. Since we rarely consider the situation of path hitting the camera sensor, it is usually 1/(s+t). The exact form of this weight is dependent on how many cases we take into consideration during bidirectional path tracing. For example, if it there is only point (delta) light in the scene, it would be 1/(s+t-1) since it is impossible to find a ray hitting the light source, reducing the number of cases by one. Naive bpdt weight is very simple, however it rarely delivers good quality comparing with other methods. As we can see from the above comparison, apart from its noisy result image, things with glass material is much dimmer due to the super low convergence rate of light tracing on such material.

The short conclusion here is that bidirectional path tracing provides no extra value with uniform weights. That is why we need to blend these intermediate results in a better way and it is multiple importance sampling that can be used to solve the very issue.

The original form of MIS weight factor introduced in Eric Veach’s thesis is like this:

$$ \tag{10} \begin{array} {lcl} w_{s,t} & = & \dfrac{p_{s,t}^2}{\Sigma_{i=0}^{s+t} (p_{i,s+t-i}^2)} \\ & = & \dfrac{1}{\Sigma_{i=0}^{s+t}((p_{i,s+t-i}/p_{s,t})^2)} \end{array} $$

Calculating all these pdfs directly is pretty boring and can easily introduce some subtle bugs which is very hard to be found. Instead of doing so, we simplify the equation first before actually implementing these weight evaluation.

Since most of the components in $ p_{i,t+s-i} $ and $ p_{i+1,t+s-i-1} $ are similar except those around the connection edge, the ratio is much simpler comparing with evaluating those two pdfs first and doing the divide later.

$$ \tag{11} \dfrac{p_{i+1,s+t-i-1}}{p_{i,s+t-i}} = \dfrac{\overrightarrow{p_i}(\bar{y})}{\overleftarrow{p_i}(\bar{y})} $$

Suppose vertex 0 is on the camera sensor. By defining the following two terms, we can put equation 10 in a more simpler form.

$$ \tag{12} w_{camera,s-1}=\Sigma_{i=0}^{s-1}(p_{i,s+t-i}/p_{s,t})^2 $$ $$ \tag{13} w_{light,t-1}=\Sigma_{i=s+1}^{s+t}(p_{i,s+t-i}/p_{s,t})^2 $$ $$ \tag{14} \begin{array} {lcl} w_{s,t} & = & \dfrac{p_{s,t}^2}{\Sigma_{i=0}^{s+t} (p_{i,s+t-i}^2)} \\ & = & \dfrac{1}{\Sigma_{i=0}^{s+t}((p_{i,s+t-i}/p_{s,t})^2)} \\ & = &\dfrac{1}{\Sigma_{i=0}^{s-1}((p_{i,s+t-i}/p_{s,t})^2) + 1 + \Sigma_{i=s+1}^{s+t}((p_{i,s+t-i}/p_{s,t})^2) } \\ & = & \dfrac{1}{w_{camera,s-1}+1+w_{light,t-1}} \end{array} $$

The evaluation of MIS weight is to evaluate these w terms given two specific sub-paths. Luckily, these two terms can be recorded progressively as we trace rays in the scene.

$$ \tag{15} w_{camera,i}=\dfrac{\overleftarrow{p_i}(\bar{y})}{\overrightarrow{p_i}(\bar{y})}(w_{camera,i-1}+1) $$ $$ \tag{16} w_{light,i}=\dfrac{\overrightarrow{p_{s+t-i}}(\bar{y})}{\overleftarrow{p_{s+t-i}}(\bar{y})}(w_{light,i-1}+1) $$

At a first look, they seem pretty different to each other. Care needs to be paid for each path differently. However they are actually the same. If the rays are generated from light sources instead of camera, we actually have the following equation 17:

$$ \tag{17} w_{light,i}=\dfrac{\overleftarrow{p_i}(\bar{y})}{\overrightarrow{p_i}(\bar{y})}(w_{light,i-1}+1) $$

A subtle difference is the pdf evaluation. With regard to the camera weight, forward pdf means pdf of sampling a direction from vertex, which is nearer to the camera vertex in term of path, to the next vertex. Vice versa. However for the light weight, forward pdf means pdf of sampling a direction from vertex, which is nearer to the light, instead of the camera vertex, to the next vertex. And what is also inverse is the index of vertex, vertex 0 means the light vertex in the former case, while it is camera sensor vertex in the latter case. Since they obey exact the same rule from their own perspective, I’m gonna drop the subscript.

$$ \tag{18} w_{i}=\dfrac{\overleftarrow{p_i}(\bar{y})}{\overrightarrow{p_i}(\bar{y})}(w_{i-1}+1) $$

There are two issues blocking us from evaluating the term directly, the $ \overleftarrow{p_i}(\bar{y})$ is unknown because next vertex is not traced yet, neither the pdf w.r.t solid angle, nor the directional g-term can be calculated before we have a clue of what the next vertex is. Another subtle issue is hidden in the $ w_{i-1} $ term, to evaluate this term, we need to know the pdf w.r.t solid angle from vertex i to i-1, sadly it is also determined by vertex i+1 because that’s where the reverse input direction is for the brdf. In order to avoid those terms, it is defined the following way:

$$ \tag{19} w_{i}=\overleftarrow{p_i}(\bar{y})(\underbrace{\dfrac{w_{i-1}}{\overrightarrow{p_i}(\bar{y})}}_{\overleftarrow{p_{\sigma,i-1}} \boxed{vc_i}}+\underbrace{\dfrac{1}{\overrightarrow{p_i}(\bar{y})}}_{\boxed{vcm_i}}) $$

From this equation, we can see that both VC and VCM can be calculated for the current vertex because those which can’t be calculated are avoided in the equation. This simply give us the following equation:

$$ \tag{20} vcm_i = \dfrac{1}{\overrightarrow{p_i}} $$ $$ \tag{21} vc_i=\dfrac{\overleftarrow{g_{i-1}}}{\overrightarrow{p_i}}(vcm_{i-1}+\overleftarrow{p_{\sigma,i-2}}vc_{i-1}) $$

These two terms can be recorded once we find a vertex along the path for each vertex. For the very first vertex on the light source and camera sensor, we define them the following way:

$$ \tag{22} vcm_{camera,1} = \dfrac{n_{samples}}{\overrightarrow{p_1}} $$ $$ \tag{23} vc_{camera,1} = 0 $$ $$ \tag{24} vcm_{light,1} = \dfrac{1}{\overrightarrow{p_1}} $$ $$ \tag{25} vc_{light,1} = \dfrac{\overleftarrow{g_0}}{\overrightarrow{p_0}\overrightarrow{p_1}} $$

We have the initial values for those terms, we only need to evaluate them progressively as we trace along the path. The only thing left is how we use them to evaluate the MIS weight. There are four cases to be consider:

Case 1: s > 1 and t > 1. This is the most common case in bidirectional path tracing, it actually connects two traced vertices from each side.

$$ \tag{26} w_{camera,s-1}=\overleftarrow{p_{s-1}}(vcm_{s-1}+\overleftarrow{p_{\sigma,s-2}}vc_{s-1}) $$ $$ \tag{27} w_{light,t-1}=\overleftarrow{p_{t-1}}(vcm_{t-1}+\overleftarrow{p_{\sigma,t-2}}vc_{t-1}) $$

Case 2: t = 0. This is the case where eye path hits area light source.

$$ \tag{28} w_{camera,s-1}= \overleftarrow{p_{s-1}}( vcm_{s-1}+\overleftarrow{p_{\sigma,s-2}}vc_{s-1}) $$ $$ \tag{29} w_{light,t-1}=0 $$

Case 3: t = 1. This is the case only one vertex is in the light sub-path.

$$ \tag{30} w_{camera,s-1}=\overleftarrow{p_{s-1}}(vcm_{s-1}+\overleftarrow{p_{\sigma,s-2}}vc_{s-1}) $$ $$ \tag{31} w_{light,t-1}=\dfrac{\overleftarrow{p_0}}{\overrightarrow{p_0}} $$

Case 4: s = 1. This is the light tracing case.

$$ \tag{32} w_{camera,s-1}=0 $$ $$ \tag{33} w_{light,t-1}=\dfrac{\overleftarrow{p_{t-1}}}{n_{sample}}(vcm_{t-1}+\overleftarrow{p_{\sigma,t-2}}vc_{t-1}) $$

So far we’ve already knew how to calculate these complex MIS weight in an elegant way, which saves much time with little memory overhead of two float numbers at each vertex. Since we only need to store a whole sub-path from one side, the two floating number memory overhead is barely noticeable.

Special Handling for Light

I have five typical type of light source in my renderer, point light, spot light, directional light, area light and sky light. Each has different properties and some of them need special treatment in a bidirectional path tracer.

Delta light

In term of light size, point light, spot light and distant light has no physical surface at all. Although these lights are not real at all in the real world, they are pretty useful in computer graphics. Note skylight has a fake surface of an sphere facing inside the world, so it can’t be count as delta light. Delta light has one very special property, it can’t be hit by random ray traced from anywhere, even if it actually hits the exact point, not to mention how small the chance is.

In this very case, we are losing the $ \overleftarrow{p_0} $ term when tracing from delta light sources. That give the following condition for delta light source:

$$ \tag{34} vc_i = 0 $$

Infinite light

In term of distance between light source and target vertex, distant light and sky light need special handling because there is actually no real surface for these light sources and vertices sampled on these light sources can be arbitrarily far.

We’ll start from sky light first. A sky sphere is used in my render to simulate the radiance distribution of the whole sky. Even for a physical based renderer, a sky light is actually not 100% accurate. For each point to be shaded, it is always the center of the whole skysphere, no matter where the vertex is. Since we are simulating the radiance far away from the whole scene, it introduces little visual artifact that is noticeable.

To sample a point on a sky light source, we first sample a direction from the target vertex, which is always (0,0,0) in sky sphere’s space. After a direction is sampled, we can evaluate the radiance along the inverse direction. 

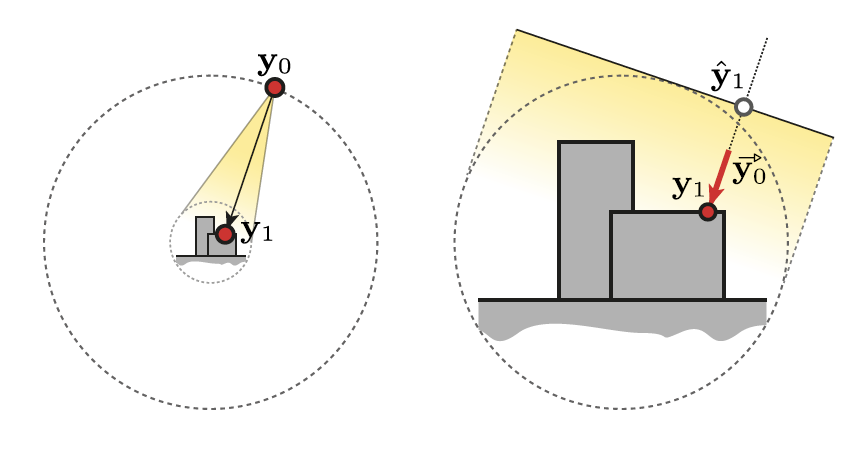
Then we need to sample a point from a plane that is perpendicular to the direction and also the tangent plane of the bounding sphere of the scene. What we only need to know is the radius of the sphere since it can be arbitrary.

Luckily we have a very nice property for sky light, as I mentioned each point to be shaded is at the center of the sky sphere. That said the distance in directional g-term is exactly the same no matter which direction it is. With the following hack, we can ignore the radius value in MIS weight.

$$ \tag{35} \overrightarrow{p_0} = \overleftarrow{p_{\sigma,origin\rightarrow y_0}} $$ $$ \tag{36} \overleftarrow{p_0}=\overleftarrow{p_{\sigma,0}} $$ $$ \tag{37} \overleftarrow{g_0}=1 $$ $$ \tag{38} \overrightarrow{p_1}=p_a(\hat{y_1}) cos\theta_{1\rightarrow 0} $$

That works because the $ \overleftarrow{p_0} $ and $ \overrightarrow{p_0} $ always appear in pair and the g-terms just get canceled with each other.  After a direction is picked, there is really no g-term available in the pdf ( $ \overrightarrow{p_1} $ ) because the direction is fixed. And the radius value totally gets vanished. Since we need to calculate shadow, we still need to setup a number for this radius value, however it doesn’t have anything to do with MIS weight and Monte Carlo estimation. Any number larger than the radius of scene bounding sphere can be fine.

Direction light is very similar except the fact that we don’t need to sample a direction in the first place because it is fixed. The others are totally the same.

Implementing Naive BDPT for Comparison

It is the power heuristic we mentioned above. In a practical MIS bidirectional path tracer, we always wrap some components of MIS weight, so that we can easily switch between balanced heuristic and power heuristic.

However a naive BDPT implementation doesn’t need to be done separately because we can just set the exponent with the value of 0. It will make your code cleaner and shorter if you also want naive bidirectional path tracer for comparison.

Reference:

[1] Robust Monte Carlo Methods For Light Transport Simulation. Eric Veach
[2] Small VCM renderer
[3] Calculating the directional probability of primary rays
[4] Bidirectional path tracing
[5] Wonderball
[6] Implementation of bidirectional ray tracing algorithm